Uncertainty Quantification and Optimization with Hybrid Models
Multi-scale modeling frameworks generally employ reduced order, surrogate or scale-bridging models to maintain computational tractability. The explicit quantification, propagation, and mitigation of uncertainties (i.e. information loss) across length and timescales due to the use of these surrogate models is an exciting field of research with the potential to bridge the gap between molecular engineering and the implementation of scalable technologies.
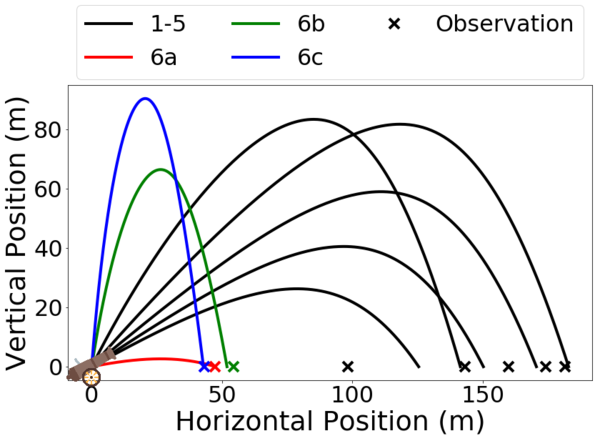
A cartoon showing the generation of training data for the ballistic firing example. x marks the observed distance traveled and includes observation error
In our work so far, using ballistic firing as an example, we have demonstrated the use of Bayesian hybrid models to account for model inadequacy. Bayesian hybrid models fuse physics-based insights with machine learning constructs to correct for systematic bias i.e. physical phenomena unaccounted for by the model, say, due to simplifying assumptions. We propose a workflow for Bayesian model calibration to fit data to the hybrid model and estimate model parameters. We then use the posterior from the hybrid model to compute optimal firing conditions to hit a target using a single-stage stochastic program. Our studies find that Bayesian hybrid models outperform pure physics-based or machine learning models for decision making under uncertainty and thereby argue that hybrid models are an emerging paradigm for decision making under uncertainty.

The hybrid model performs better than the pure physics or pure data model. The physics from the simple model makes the model sensitive to firing angle and the GP (machine-learning component) accounts for neglected air resistance to provide optimal firing conditions.
Recently, we have extended the framework proposed in the ballistics example to a reactions case study.
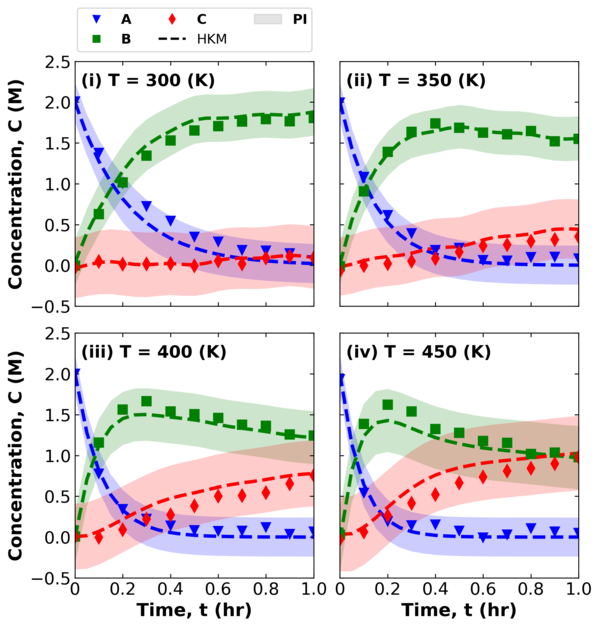
Hybrid model predictions with epistemic, aleatoric, and parameter uncertainty.
In the future, we would like to explore three key areas using Bayesian hybrid models:
1) Simultaneous physically-meaningful and GP parameter estimation via semiparametric regression
2) Adaptive design of experiments utilizing acquisition functions to manage the tradeoff between exploration and exploitation
3) Scalability of hybrid kinetic models; computationally efficient variational inference algorithms for model calibration
Related Publications
Kyla D. Jones, Elvis A. Eugene, Alexander W. Dowling. Decision Making with Hybrid Models Under Parameter and Epistemic Uncertainty: Reactor Optimization Case Study (2023). Foundations of Computer Aided Process Operations / Chemical Process Control (FOCAPO/CPC 2023).
Elvis A. Eugene*, Kyla D. Jones, Jialu Wang, and Alexander W. Dowling. Optimization Under Uncertainty with Bayesian Hybrid Models. AIChE Annual Meeting. Phoenix, AZ. November 17, 2022. [link]
Kyla D. Jones*, Elvis A. Eugene, and Alexander W. Dowling. Optimization Under Uncertainty with Bayesian Hybrid Models. INFORMS Annual Meeting. Indianapolis, IN. Flash Talk. October 19, 2022. [link]
Kyla D. Jones*, Elvis A. Eugene, and Alexander W. Dowling. Uncertainty Quantification and Optimization with Bayesian Hybrid Models for Chemical Sciences, Engineering, and Beyond. SIAM Mathematics of Data Science. San Diego, CA. Poster. September 28, 2022. [link]
Jialu Wang, Elvis A. Eugene, and Alexander W. Dowling. Scalable Stochastic Programming with Bayesian Hybrid Models (2022). 14th International Symposium on Process Systems Engineering (PSE2021+). Ed. by Y. Yamashita, M. Kano. [file]
Elvis A. Eugene* and Alexander W. Dowling. Decision-Making Under Epistemic Uncertainty Using Bayesian Hybrid Models. AIChE Annual Meeting, Boston, MA, November 8, 2021. [link]
Elvis A. Eugene*, Xian Gao, and Alexander W. Dowling. Bayesian Learning from Hybrid Models and Their Applications in Thermodynamics and Reaction Engineering. AIChE Annual Meeting, November 19, 2020. [link]
Elvis A. Eugene, Xian Gao, Alexander W. Dowling. Learning and Optimization with Bayesian Hybrid Models. Proceedings of the 2020 American Control Conference (ACC 2020), Submitted, https://arxiv.org/abs/1912.06269.
Support from National Science Foundation grant (CBET-1941596) "CAREER: Uncertainty Quantification and Optimization with Hybrid Models for Molecular-to-Systems Engineering"


